(1) Download time series data from Yahoo Finance (example here is to download from 2011 up to 2013), or copy the url and download in browser and save as csv files
- getstockdata.sh Select all
curl "http://ichart.finance.yahoo.com/table.csv?s=MSFT&a=0&b=01&c=2011&d=11&e=31&f=2013&g=d" > msft.csv
curl "http://ichart.finance.yahoo.com/table.csv?s=AAPL&a=0&b=01&c=2011&d=11&e=31&f=2013&g=d" > aapl.csv
curl "http://ichart.finance.yahoo.com/table.csv?s=^IXIC&a=0&b=01&c=2011&d=11&e=31&f=2013&g=d" > nasdaq.csv
curl "http://ichart.finance.yahoo.com/table.csv?s=GOOG&a=0&b=01&c=2011&d=11&e=31&f=2013&g=d" > goog.csv
### or use wget "http://ichart.finance.yahoo.com/table.csv?s=MSFT&a=0&b=01&c=2011&d=11&e=31&f=2013&g=d" -O msft.csv
(2) Run script in R, you can use source("stocks.r")
- stocks.r Select all
msft <- read.csv("msft.csv")
aapl <- read.csv("aapl.csv")
goog <- read.csv("goog.csv")
nasdaq <- read.csv("nasdaq.csv")
stocks <- nasdaq[,c("Date","Close")]
colnames(stocks)[2] <- "NASDAQ"
stocks["MSFT"] <- NA
stocks$MSFT <- msft$Close
stocks["AAPL"] <- NA
stocks$AAPL <- aapl$Close
stocks["GOOG"] <- NA
stocks$GOOG <- goog$Close
(3) Do some analysis in R
- analysis.r Select all
### plot Data
plot(aapl$Date, aapl$Close)
cor(goog[c("Open")],aapl[c("Open")])
summary(stocks)
str(stocks)
pairs(stocks[-1])
cor(stocks[-1])
cov(stocks[-1])
eigen(cor(stocks[-1]))
### Do linear regression
mod1 <- lm(NASDAQ ~ MSFT + AAPL + GOOG, data=stocks)
summary(mod1)
?summary.lm
### Confidence Limits on the Estimated Coefficients
confint(mod1)
summary.aov(mod1)
### Prediction of mean response for cases like this...
predict(mod1, list(MSFT=30,AAPL=400,GOOG=800), interval="conf")
### Prediction for a single new case...
predict(mod1, list(MSFT=30,AAPL=400,GOOG=800), interval="pred")
mod2 = update(mod1,.~.-AAPL)
summary(mod2)
(prediction <- c(1,30,800) * coef(mod2))
sum(prediction)
### Compare two models
anova(mod1, mod2)
### Regression Diagnostics
par(mfrow=c(2,2)); plot(mod1); par(mfrow=c(1,1))
(4) Stepwise Regression in R
- stepwise.r Select all
###retrieve more stocks data directly using R as below
intc <- read.csv("http://ichart.finance.yahoo.com/table.csv?s=INTC&a=0&b=01&c=2011&d=11&e=31&f=2013&g=d")
amzn <- read.csv("http://ichart.finance.yahoo.com/table.csv?s=AMZN&a=0&b=01&c=2011&d=11&e=31&f=2013&g=d")
###update model and do stepwise regression
stocks$INTC <- intc$Close
stocks$AMZN <- amzn$Close
mod3 <- lm(NASDAQ ~ MSFT + AAPL + GOOG + INTC + AMZN, data=stocks)
step(mod3, direction="both")
summary(mod3)
summary(step(mod3, direction="both"))
(5) Delta Normal VaR and ES for a single asset using R
Reference (VaR using Excel) : http://www.youtube.com/watch?v=ZrKmVC-Ede8
- DNVaR1.r Select all
# get the time series of AAPL with Closed Price
aapl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=AAPL&a=2&b=23&c=2012&d=2&e=23&f=2013&g=d");
# calculate log returns, note the -log sign below
aapl.logreturn = c(diff(-log(aapl$Close)));
# calculate VaR for 95% confidence interval, VaR is 0.03513197
qnorm(0.95)*sd(aapl.logreturn)-mean(aapl.logreturn);
#alternatively, qnorm(p=0.95, sd=sd(aapl.logreturn), mean=mean(aapl.logreturn));
# with a single asset of say $1M, the calculated Delta Normal VaR is $35,131.97
sprintf("%5.2f", 1e+06*(qnorm(0.95)*sd(aapl.logreturn)-mean(aapl.logreturn)));
#Expected Shortfall(ES) for Normal Distribution = $62,227.24
v <- qnorm(p=0.95, sd=sd(aapl.logreturn), mean=mean(aapl.logreturn))
tailExp <- integrate(function(x)
x * dnorm(x, mean=mean(aapl.logreturn),
sd=sd(aapl.logreturn)),
lower=-Inf, upper=v)$value / (1-0.95)
-tailExp * 1e+06
(6) Delta Normal VaR for a portfolio of assets using R
Reference (Portfolio VaRs using Excel) : https://www.youtube.com/watch?v=GqczSHRUaDk
- DNVaR2.r Select all
# get the time series of MSFT, GOOG, AAPL, ORCL and IBM
msft <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=MSFT&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
goog <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=GOOG&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
aapl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=AAPL&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
orcl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=ORCL&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
ibm <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=IBM&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
# calculate log returns from Closed Prices
msft.logreturn = c(diff(-log(msft$Close)));
goog.logreturn = c(diff(-log(goog$Close)));
aapl.logreturn = c(diff(-log(aapl$Close)));
orcl.logreturn = c(diff(-log(orcl$Close)));
ibm.logreturn = c(diff(-log(ibm$Close)));
# calculate the individual volatility
logreturns <- data.frame(msft.logreturn, goog.logreturn, aapl.logreturn, orcl.logreturn, ibm.logreturn);
sapply(logreturns,sd);
# calculate the individual VaR using Matrix and with position of $1M each using correlation matrix
VaR1 = (1e+06*sapply(logreturns,sd)) %*% cor(logreturns);
# calculate the Dollar Variance of the Portfolio
VaR2 = VaR1 %*% (1e+06*sapply(logreturns,sd));
# Square Root Portfolio Variance to calculate the Delta Normal 1-day Portfolio VaR for 95% confidence interval. The result is $119,605.5
qnorm(0.95) * sqrt(VaR2);
#Alternatively, the variance-cov method is demo here
v1 = cov(logreturns) %*% rep(1e+06,5);
v2 = rep(1e+06,5) %*% v1;
sqrt(v2)*qnorm(0.95);
# Portfolio VaR for 10 days
sqrt(v2)*qnorm(0.95)* sqrt(10);
(6.1) Delta Normal VaR and ES for a portfolio of assets using R
Using : simple return instead of log return
- DNVaR2.r Select all
# get the time series of MSFT, GOOG, AAPL, ORCL and IBM
msft <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=MSFT&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
yhoo <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=YHOO&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
aapl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=AAPL&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
orcl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=ORCL&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
ibm <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=IBM&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
# calculate simple returns from Closed Prices
#msft.simplereturn = -diff(msft$Close)/msft$Close[-length(msft$Close)];
#yhoo.simplereturn = -diff(yhoo$Close)/goog$Close[-length(yhoo$Close)];
#aapl.simplereturn = -diff(aapl$Close)/aapl$Close[-length(aapl$Close)];
#orcl.simplereturn = -diff(orcl$Close)/orcl$Close[-length(orcl$Close)];
#ibm.simplereturn = -diff(ibm$Close)/ibm$Close[-length(ibm$Close)];
msft.simplereturn = msft$Close[-nrow(msft)] / msft$Close[-1] -1;
yhoo.simplereturn = yhoo$Close[-nrow(yhoo)] / yhoo$Close[-1] -1;
aapl.simplereturn = aapl$Close[-nrow(aapl)] / aapl$Close[-1] -1;
orcl.simplereturn = orcl$Close[-nrow(orcl)] / orcl$Close[-1] -1;
ibm.simplereturn = ibm$Close[-nrow(ibm)] / ibm$Close[-1] -1;
# plot the histogram, assume different stock position
simplereturns <- data.frame(msft.simplereturn,yhoo.simplereturn,aapl.simplereturn,orcl.simplereturn,ibm.simplereturn);
hist(as.matrix(simplereturns) %*% c(1e+06, 1e+05, 5e+03, 9e+04, 3e+05),col="green");
# calculate the individual volatility
simplereturns <- data.frame(msft.simplereturn, yhoo.simplereturn, aapl.simplereturn, orcl.simplereturn, ibm.simplereturn);
sapply(simplereturns,sd);
#using the variance-covariance method with different stock position to calculate VaR $35,473.23
v1 = cov(simplereturns) %*% c(1e+06, 1e+05, 5e+03, 9e+04, 3e+05);
v2 = c(1e+06, 1e+05, 5e+03, 9e+04, 3e+05) %*% v1;
sqrt(v2)*qnorm(0.95);
# Portfolio VaR for 10 days
sqrt(v2)*qnorm(0.95)* sqrt(10);
#calculate the ES $21,986.07
m <- sapply(simplereturns,mean) %*% c(1e+06, 1e+05, 5e+03, 9e+04, 3e+05);
v <- qnorm(p=0.95, sd=sqrt(v2), mean=m);
- integrate(function(x)
x * dnorm(x, mean=m,
sd=sqrt(v2)),
lower=-Inf, upper=v)$value / (1-0.95)
# use PerformanceAnalytics to calculate VaR and ES
require(PerformanceAnalytics)
stockportfolio.ts <- as.xts(data.frame(msft$Close,yhoo$Close,aapl$Close,orcl$Close,ibm$Close), order.by = as.Date(msft$Date,"%Y-%m-%d"))
# calculate VaR $34,289.08
VaR(R = na.omit(Return.calculate(stockportfolio.ts, method="discrete")), p = 0.95, method = "gaussian", portfolio_method = "component", weights = c(1e+06, 1e+05, 5e+03, 9e+04, 3e+05))
# calculate ES $43,300.71
ETL(R = na.omit(Return.calculate(stockportfolio.ts, method="discrete")), p = 0.95, method = "gaussian", portfolio_method = "component", weights = c(1e+06, 1e+05, 5e+03, 9e+04, 3e+05))
(7) Historical Simulation VaR for a single asset using R
Reference (Historical Simulation using Excel) : http://www.youtube.com/watch?v=6Nolb4-iRSI
- HSVaR1.r Select all
# get the time series of GOOG with Closed Price
goog <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=GOOG&a=1&b=25&c=2008&d=6&e=18&f=2008&g=d")
# calculate log returns, using natural log
goog.logreturn = c(diff(-log(goog$Close)));
# plot histogram
hist(goog.logreturn, breaks=seq(-.11,.19,by=.01), col="green");
#show the first 10 items in ascending order
head(sort(goog.logreturn),n=10);
# find volatility for 5% percentile, that is -4.10867%
quantile(goog.logreturn,0.05);
#Historical Simulation VaR for $1,000 is 4.10867
-quantile(goog.logreturn,0.05)*1000;
# find historical volatility for the 102 observations
sd(goog.logreturn)*sqrt(length(goog[,1]));
(7.1) Historical Simulation VaR for a single asset using R
Reference : Using the same data as per (5) above
- HSVaR11.r Select all
# get the time series of AAPL with Closed Price
aapl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=AAPL&a=2&b=23&c=2012&d=2&e=23&f=2013&g=d");
# calculate log returns, note the -log sign below
aapl.logreturn = c(diff(-log(aapl$Close)));
# calculate simple returns
aapl.simplereturn = aapl$Close[-nrow(aapl)] / aapl$Close[-1] -1;
# plot histogram and density curve
hist(aapl.logreturn,breaks=seq(-.15,.1,by=.02), col="green",freq=FALSE,main="Asset Returns", xlab="Return%",xlim=range(-0.15,0.1),ylim=range(0,28));lines(density(aapl.logreturn),col="red", lty="dotted",panel.last=abline(v=quantile(aapl.logreturn, 0.05), col="darkred",lwd=3)); mtext("95% C.I.",side=3,line=-3,adj=0.40,col="darkred");
#show the first 15 items in ascending order
head(sort(aapl.logreturn),n=15);
# find VaR for 5% percentile, volatility is 0.03205498 = $32,054.98
-quantile(aapl.logreturn,0.05)*1e+06;
# find VaR for 5% percentile, volatility is 0.03205498 = $31,546.66
-quantile(aapl.simplereturn,0.05)*1e+06;
# with a single asset of say $1M, the calculated Historical Simulation VaR is $32,054.98 comparing with the result of Delta Normal VaR of $35,131.97 as per (5) above
sprintf("%5.2f", 1e+06*-quantile(aapl.logreturn,0.05));
# calculate ES $46,965.9 for log returns
-mean(aapl.logreturn[aapl.logreturn <= quantile(aapl.logreturn, 0.05)])*1e+6;
# calculate ES $45,565.73 for simple returns
-mean(aapl.simplereturn[aapl.simplereturn <= quantile(aapl.simplereturn, 0.05)])*1e+6;
(7.2) Historical Simulation VaR for a single asset using R and Package PerformanceAnalytics
Reference : http://cran.at.r-project.org/web/packages/PerformanceAnalytics/
http://cran.r-project.org/web/packages/quantmod/
- HSVaR12.r Select all
#install.packages("PerformanceAnalytics");
require(PerformanceAnalytics)
# get the time series of AAPL with Closed Price
aapl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=AAPL&a=2&b=23&c=2012&d=2&e=23&f=2013&g=d");
# convert to time series
aapl.ts <- as.xts(aapl$Close, order.by = as.Date(aapl$Date,"%Y-%m-%d"));
# calculate VaR $32,054.98 for log returns
-VaR(Return.calculate(aapl.ts, method="log"),p=.95,method="historical") * 1e+06;
# calculate VaR $31,546.66 for simple returns
-VaR(Return.calculate(aapl.ts, method="discrete"),p=.95,method="historical") * 1e+06;
# calculate ES $46,965.9 for log returns
-ETL(Return.calculate(aapl.ts, method="log"),p=.95,method="historical") * 1e+06;
# calculate ES $45,565.73 for simple returns
-ETL(Return.calculate(aapl.ts, method="discrete"),p=.95,method="historical") * 1e+06;
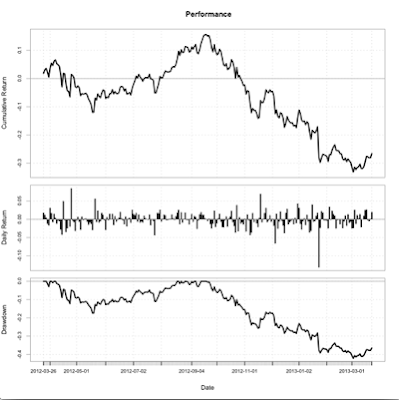
#plot PerformanceSummary using Package PerformanceAnalytics
charts.PerformanceSummary(Return.calculate(aapl.ts, method="log"));
#plot the time series chart using Package quantmod
#install.packages("quantmod");
require("quant mod");
chartSeries(aapl.ts, theme = chartTheme("white"), TA = c(addBBands(),addTA(RSI(aapl.ts))));
(7.3) Calculate VaR for a single asset using Monte carlo simulation: Brownian motion
Require : http://cran.at.r-project.org/web/packages/PerformanceAnalytics/
- MCVaR.r Select all
#install.packages("PerformanceAnalytics");
require(PerformanceAnalytics)
# get the time series of AAPL with Closed Price
aapl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=AAPL&a=2&b=23&c=2012&d=2&e=23&f=2013&g=d");
# convert to time series
aapl.ts <- as.xts(aapl$Close, order.by = as.Date(aapl$Date,"%Y-%m-%d"));
# calculate VaR $32,054.98 for log returns
-VaR(Return.calculate(aapl.ts, method="log"),p=.95,method="historical") * 1e+06;
# calculate VaR $3x,xxx (will print 3 iterations) using random 250 samples log returns generated based on sd and mean of AAPL
aapl.logreturn = c(diff(-log(aapl$Close)));
for (i in 1:3) {print (-VaR(as.xts(rnorm(250, sd=sd(aapl.logreturn), mean=mean(aapl.logreturn)),order.by=as.Date(aapl$Date,"%Y-%m-%d")),p=.95,method="historical") * 1e+06)};
# calculate VaR using random 1000 samples log returns generated based on sd and mean of AAPL
for (i in 1:3) {print (-VaR(as.xts(rnorm(1000, sd=sd(aapl.logreturn), mean=mean(aapl.logreturn)),order.by=as.Date(Sys.Date():(Sys.Date()+1000-1))),p=.95,method="historical") * 1e+06)};
# calculate VaR (will print 3 iterations) using random 250 samples log returns generated
# based on the assumptions of annual return drift=0.10 and annual return volatility=0.40
# daily volatility = annual volatility / sort(T)
# daily mean drift = annual drift/T - 0.5 * sd^2
# model reference from http://www.youtube.com/watch?v=e79OtCamxD0
for (i in 1:3) {print (-VaR(as.xts(rnorm(250, sd=0.40/sqrt(250), mean=(0.10/250)-0.5*((0.40/sqrt(250))^2)),order.by=as.Date(aapl$Date,"%Y-%m-%d")),p=.95,method="historical") * 1e+06)};
# calculate VaR (will print 3 iterations) using random 1000 samples log returns generated
# based on the assumptions of annual return drift=0.10 and a higher annual return volatility=0.60
for (i in 1:3) {print (-VaR(as.xts(rnorm(1000, sd=0.60/sqrt(250), mean=(0.10/250)-0.5*((0.60/sqrt(250))^2)),order.by=as.Date(Sys.Date():(Sys.Date()+1000-1))),p=.95,method="historical") * 1e+06)};
# plot the simulated prices from one instance of simulation
aapl.mc.logreturns = rnorm(1000, sd=0.60/sqrt(250), mean=(0.10/250)-0.5*((0.60/sqrt(250))^2));
plot(as.xts(c(1,exp(cumsum(aapl.mc.logreturns))) * tail(aapl$Close,n=1),order.by=as.Date(as.Date(c("2010-01-01")):(as.Date(c("2010-01-01"))+1000))),main="Simulated Price");
(8) Historical Simulation VaR for a portfolio of assets using R
Reference : Using the same data as per (6) Delta Normal VaR for a portfolio of assets
- HSVaR2.r Select all
# get the time series of MSFT, GOOG, AAPL, ORCL and IBM
msft <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=MSFT&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
goog <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=GOOG&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
aapl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=AAPL&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
orcl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=ORCL&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
ibm <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=IBM&a=5&b=14&c=2011&d=5&e=8&f=2012&g=d")
# calculate log returns from Closed Prices
msft.logreturn = c(diff(-log(msft$Close)));
goog.logreturn = c(diff(-log(goog$Close)));
aapl.logreturn = c(diff(-log(aapl$Close)));
orcl.logreturn = c(diff(-log(orcl$Close)));
ibm.logreturn = c(diff(-log(ibm$Close)));
# plot the histogram and density
logreturns <- data.frame(msft.logreturn, goog.logreturn, aapl.logreturn, orcl.logreturn, ibm.logreturn);
hist(as.matrix(logreturns) %*% rep(1e+06,5),col="green",freq=FALSE);
lines(density(as.matrix(logreturns) %*% rep(1e+06,5)),col="red")
# find VaR for 5% percentile, that is $109,409.9 and comparing with the result of Delta Normal VaR of $119,605.5 as per (6) above
-quantile(as.matrix(logreturns) %*% rep(1e+6,5), 0.05);
(8.1) Historical Simulation VaR and ES for a portfolio of assets using R
Using : simple return instead of log return
Calculate : Incremental VaR, Marginal VaR and Component VaR
- HSVaR250.r Select all
# get the time series of MSFT, YHOO, AAPL, ORCL and IBM for 251 trading days
msft <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=MSFT&a=3&b=3&c=2013&d=2&e=31&f=2014&g=d")
yhoo <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=YHOO&a=3&b=3&c=2013&d=2&e=31&f=2014&g=d")
aapl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=AAPL&a=3&b=3&c=2013&d=2&e=31&f=2014&g=d")
orcl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=ORCL&a=3&b=3&c=2013&d=2&e=31&f=2014&g=d")
ibm <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=IBM&a=3&b=3&c=2013&d=2&e=31&f=2014&g=d")
# calculate simple returns from Closed Prices
msft.simplereturn = msft$Close[-nrow(msft)] / msft$Close[-1] -1;
yhoo.simplereturn = yhoo$Close[-nrow(yhoo)] / yhoo$Close[-1] -1;
aapl.simplereturn = aapl$Close[-nrow(aapl)] / aapl$Close[-1] -1;
orcl.simplereturn = orcl$Close[-nrow(orcl)] / orcl$Close[-1] -1;
ibm.simplereturn = ibm$Close[-nrow(ibm)] / ibm$Close[-1] -1;
# plot the histogram
simplereturns <- data.frame(msft.simplereturn,yhoo.simplereturn,aapl.simplereturn,orcl.simplereturn,ibm.simplereturn);
hist(as.matrix(simplereturns) %*% rep(1,5),col="green",freq=FALSE);
lines(density(as.matrix(simplereturns) %*% rep(1,5)),col="red");
# find VaR for 5% percentile, that is $71,726.65
-quantile(as.matrix(simplereturns) %*% rep(1e+6,5), 0.05);
# find Incremental VaR for each asset by removing each asset from the portfolio
# Incremental VaR : MSFT $3396.407; YHOO $19522.17; AAPL $10691.23; ORCL $12628.08; IBM $10749.8
Iport = matrix(1e+06, nrow=5, ncol=5);
diag(Iport)=0;
for (i in 1:5) {print(quantile(as.matrix(simplereturns) %*% (Iport)[i,], 0.05) -quantile(as.matrix(simplereturns) %*% rep(1e+6,5), 0.05))};
# Marginal VaR by list out the 13th element sort by portfolio return column
# msft.simplereturn yhoo.simplereturn aapl.simplereturn orcl.simplereturn ibm.simplereturn portfolio
#45 -0.02118989 -0.03323661 0.008112513 -0.01670709 -0.009686039 -0.07270712
returns <- data.frame(simplereturns, portfolio=as.matrix(simplereturns) %*% rep(1,5) )
tail(head(returns[order(returns$portfolio),],n=length(returns[,1])*0.05+1),n=1)
# Component VaR by multiplying Marginal VaR by the weight of each asset
# msft.simplereturn yhoo.simplereturn aapl.simplereturn orcl.simplereturn ibm.simplereturn portfolio
#45 -21189.89 -33236.61 8112.513 -16707.09 -9686.039 -72707.12
tail(head(returns[order(returns$portfolio),],n=250*0.05+1),n=1) * 1e+6
#find Expected Shortfall (ES) that is $103,035.5
m <- as.matrix(simplereturns) %*% rep(1e+6,5);
v <- quantile(m, 0.05);
-mean(m[m <= v]);
# plot all
hist(as.matrix(simplereturns) %*% rep(1,5),col="green",freq=FALSE,main="Portfolio Returns", xlab="Return%",xlim=range(-0.2,0.15),ylim=range(0,10));lines(density(as.matrix(simplereturns) %*% rep(1,5)),col="red", lty="dotted",panel.last=abline(v=quantile(as.matrix(simplereturns) %*% rep(1,5), 0.05), col="darkred",lwd=3)); mtext("95% C.I.",side=3,line=-3,adj=0.28,col="darkred");
#plot all plus superimposed normal distribution curve
xvals <- seq(from=-0.15, to=0.15,length=100)
hist(as.matrix(simplereturns) %*% rep(1,5),col="green",freq=FALSE,main="Portfolio Returns", xlab="Return%",xlim=range(-0.2,0.15),ylim=range(0,10));lines(density(as.matrix(simplereturns) %*% rep(1,5)),col="red", lty="dotted",panel.last=abline(v=quantile(as.matrix(simplereturns) %*% rep(1,5), 0.05), col="darkred",lwd=3)); mtext("95% C.I.",side=3,line=-3,adj=0.28,col="darkred");lines(xvals,dnorm(xvals,mean(as.matrix(simplereturns) %*% rep(1,5)),sd(as.vector(as.matrix(simplereturns) %*% rep(1,5)))),lwd=1,col="blue");
(8.2) Historical Simulation 10-Days VaR and ES for a portfolio of assets using R
Using : log return for 10 days and simple return for portfolio with 4 years historical data
- HSVaR10.r Select all
# get the time series of MSFT, YHOO, AAPL, ORCL and IBM for 260 trading days
msft <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=MSFT&a=2&b=20&c=2010&d=2&e=31&f=2014&g=d")
yhoo <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=YHOO&a=2&b=20&c=2010&d=2&e=31&f=2014&g=d")
aapl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=AAPL&a=2&b=20&c=2010&d=2&e=31&f=2014&g=d")
orcl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=ORCL&a=2&b=20&c=2010&d=2&e=31&f=2014&g=d")
ibm <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=IBM&a=2&b=20&c=2010&d=2&e=31&f=2014&g=d")
# calculate log returns from Closed Prices and takes first 1000 samples only
msft.logreturn10 = c(diff(-log(msft$Close),10));
yhoo.logreturn10 = c(diff(-log(yhoo$Close),10));
aapl.logreturn10 = c(diff(-log(aapl$Close),10));
orcl.logreturn10 = c(diff(-log(orcl$Close),10));
ibm.logreturn10 = c(diff(-log(ibm$Close),10));
logreturns10 <- data.frame(msft.logreturn10, yhoo.logreturn10, aapl.logreturn10, orcl.logreturn10, ibm.logreturn10)[1:1000,];
# convert to simple returns
simplereturns10 <- (exp(logreturns10)-1)
# find VaR for 5% percentile for 10 days holding period, that is $259,314.5
-quantile(as.matrix(simplereturns10) %*% rep(1e+6,5), 0.05);
#find 10-Days expected Shortfall (ES) that is $343,451.5
m <- as.matrix(simplereturns10) %*% rep(1e+6,5);
v <- quantile(m, 0.05);
-mean(m[m <= v]);
# plot all
hist(as.matrix(simplereturns10) %*% rep(1,5),col="green",freq=FALSE,main="Portfolio Returns for Holding Period 10 days", xlab="Return%",xlim=range(-0.6,0.6),ylim=range(0,4));lines(density(as.matrix(simplereturns10) %*% rep(1,5)),col="red", lty="dotted",panel.last=abline(v=quantile(as.matrix(simplereturns10) %*% rep(1,5), 0.05), col="darkred",lwd=3)); mtext("95% C.I.",side=3,line=-3,adj=0.20,col="darkred");
#List the 51st item sort by portfolio return
#587 0.004545455 0.00523416 -0.002571286 -0.003148254 -0.01536958 -0.2592768
returns10 <- data.frame(simplereturns, portfolio=as.matrix(simplereturns10) %*% rep(1,5));
tail(head(returns10[order(returns10$portfolio),],n=length(returns10[,1])*0.05+1),n=1);
(8.3) Historical Simulation VaR and ES for a portfolio of assets using R and Package PerformanceAnalytics
Backtesting : if Actual Return < Theoretical VaR
constrOptim Ref : http://www.youtube.com/watch?v=MCvz-c6UUkw
- HSVaR21.r Select all
require(PerformanceAnalytics)
# get the time series of MSFT, YHOO, AAPL, ORCL and IBM
msft <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=MSFT&a=0&b=1&c=2012&d=2&e=31&f=2014&g=d")
yhoo <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=YHOO&a=0&b=1&c=2012&d=2&e=31&f=2014&g=d")
aapl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=AAPL&a=0&b=1&c=2012&d=2&e=31&f=2014&g=d")
orcl <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=ORCL&a=0&b=1&c=2012&d=2&e=31&f=2014&g=d")
ibm <-read.csv("http://ichart.finance.yahoo.com/table.csv?s=IBM&a=0&b=1&c=2012&d=2&e=31&f=2014&g=d")
stockportfolio.ts <- as.xts(data.frame(msft$Close,yhoo$Close,aapl$Close,orcl$Close,ibm$Close), order.by = as.Date(msft$Date,"%Y-%m-%d"))
# calculate VaR 0.0215341 0.01744393 0.02875233 0.02034777 0.01493424
-VaR(Return.calculate(stockportfolio.ts[1:251], method="discrete"),p=.95,method="historical")
# calculate ES 0.02622294 0.02608046 0.03779529 0.02482448 0.02314859
-ETL(Return.calculate(stockportfolio.ts[1:251], method="discrete"),p=.95,method="historical")
# Backtesting p=0.95 assuming equal weights
# i Actual Theoretical
# 2013-06-20 368 -0.128825 0.1031542
# 2013-06-21 369 -0.1229124 0.1039837
# 2013-07-19 388 -0.1754735 0.103187
# 2013-08-27 415 -0.1080645 0.1028595
# 2014-02-03 524 -0.1150287 0.1047768
for (i in 1:(nrow(stockportfolio.ts)-251)) {
actual <- sum(na.omit(Return.calculate(stockportfolio.ts[(251+i-1):(251+i)])));
theoretical <- sum(-VaR(Return.calculate(
stockportfolio.ts[(i):(251+i-1)],method="discrete"),p=.95,method="historical"));
if (any(actual < -theoretical)) {
print(cbind(stockportfolio.ts[(251+i),0],i=251+i,Actual=actual,Theoretical=theoretical))
}
}
# Backtesting p=0.99 assuming equal weights
# i Actual Theoretical
# 2013-07-19 388 -0.1754735 0.1667104
for (i in 1:(nrow(stockportfolio.ts)-251)) {
actual <- sum(na.omit(Return.calculate(stockportfolio.ts[(251+i-1):(251+i)])));
theoretical <- sum(-VaR(Return.calculate(
stockportfolio.ts[(i):(251+i-1)],method="discrete"),p=.99,method="historical"));
if (any(actual < -theoretical)) {
print(cbind(stockportfolio.ts[(251+i),0],i=251+i,Actual=actual,Theoretical=theoretical))
}
}
# Backtesting p=0.99 assuming weights of c(30,50,200,50,50)
# i Actual Theoretical
# 2013-01-24 266 -23.5823 13.22212
# 2014-01-28 520 -13.10302 12.38539
for (i in 1:(nrow(stockportfolio.ts)-251)) {
actual <- sum(na.omit(Return.calculate(stockportfolio.ts[(251+i-1):(251+i)])) * c(30,50,200,50,50));
theoretical <- sum(-VaR(Return.calculate(
stockportfolio.ts[(i):(251+i-1)],method="discrete"),p=.99,method="historical") * c(30,50,200,50,50));
if (any(actual < -theoretical)) {
print(cbind(stockportfolio.ts[(251+i),0],i=251+i,Actual=actual,Theoretical=theoretical))
}
}
# Use constraint optimisation to find the weight of each share of the portfolio
# optimise function g and to minimise VaR
portfolioVaR <- -VaR(Return.calculate(stockportfolio.ts[1:251], method="discrete"),p=.95,method="historical");
g <- function(x) {sum(portfolioVaR* x)};
# constraint matrix
A <- matrix(c(rep(1,5),rep(-1,5),diag(1,5),diag(-1,5)),nrow=2+5+5, ncol=5, byrow=TRUE);
# constraint values : value of portfolio = 500 and shareholding for each stock > 0 that is no short selling
b <- 500 * c(0.999999,-1.000-0.000001,rep(0.000001,5),rep(-1.000-0.000001,5));
# run constrOptim with initial value of 100 each
# $par = 0.1113882 58.9182990 0.4609939 78.1495814 362.3602354
# $value = 8.045164
constrOptim(theta=rep(100,5),grad=NULL,f=g,ui=A,ci=b)
# Backtesing again and plot the graph for Actual vs. Theoretical results based on the above optimised portfolio
# i Actual Theoretical
# 2013-04-19 325 -28.85769 12.51676
# 2013-10-17 451 -24.06681 13.6749
result.frame = data.frame()
for (i in 1:(nrow(stockportfolio.ts)-251)) {
actual <- sum(na.omit(Return.calculate(stockportfolio.ts[(251+i-1):(251+i)])) * c(0.1113882,58.9182990,0.4609939,78.1495814,362.3602354));
theoretical <- sum(-VaR(Return.calculate(
stockportfolio.ts[(i):(251+i-1)],method="discrete"),p=.99,method="historical") * c(0.1113882,58.9182990,0.4609939,78.1495814,362.3602354));
if (any(actual < -theoretical )) {
print(cbind(stockportfolio.ts[(251+i),0],i=251+i,Actual=actual,Theoretical=theoretical));
};
result.frame <- rbind(result.frame, data.frame(stockportfolio.ts[(251+i),],i=(251+i), Actual=actual,Theoretical=-theoretical));
}
result.zoo <- as.zoo(result.frame)
plot(x = result.zoo[,7:8], screens = 1, main="Actual vs. Theoretical VaR", xlab = "Time", ylab = "Return", col = c("darkgreen", "red")); legend(x = "bottomright", legend = c("Actual","Theoretical"),lty=1,col=c("darkgreen", "red"));
# revise the optimisation function to include portfolioLogReturn and to minimise risk / return ratio
#$par 1.177901 111.451867 142.695042 143.658599 101.017062
portfolioLogReturn <- colSums(Return.calculate(stockportfolio.ts[1:251], method="log"),na.rm=TRUE)
g1 <- function(x) {sum(portfolioVaR * x)/sum(portfolioLogReturn * x)};
A <- matrix(c(rep(1,5),rep(-1,5),diag(1,5),diag(-1,5)),nrow=2+5+5, ncol=5, byrow=TRUE);
b <- 500 * c(0.999999,-1.000-0.000001,rep(0.000001,5),rep(-1.000-0.000001,5));
constrOptim(theta=rep(100,5),grad=NULL,f=g1,ui=A,ci=b)
# rerun backtesting with portfolio weights = c(1.177901,111.451867,142.695042,143.658599,101.017062)
result.frame = data.frame()
for (i in 1:(nrow(stockportfolio.ts)-251)) {
actual <- sum(na.omit(Return.calculate(stockportfolio.ts[(251+i-1):(251+i)])) * c(1.177901,111.451867,142.695042,143.658599,101.017062));
theoretical <- sum(-VaR(Return.calculate(
stockportfolio.ts[(i):(251+i-1)],method="discrete"),p=.99,method="historical") * c(1.177901,111.451867,142.695042,143.658599,101.017062));
if (any(actual < -theoretical )) {
print(cbind(stockportfolio.ts[(251+i),0],i=251+i,Actual=actual,Theoretical=theoretical));
};
result.frame <- rbind(result.frame, data.frame(stockportfolio.ts[(251+i),],i=(251+i), Actual=actual,Theoretical=-theoretical));
}
result2.zoo <- as.zoo(result.frame)
plot(x = result2.zoo[,7:8], screens = 1, main="Actual vs. Theoretical VaR with optimised portfolio", xlab = "Time", ylab = "Return", col = c("darkgreen", "red")); legend(x = "topleft", legend = c("Actual","Theoretical"),lty=1,col=c("darkgreen", "red"));
There is one important difference between log return and simple return is that log return is time additive and simple return is portfolio additive. (Reference : http://www.youtube.com/watch?v=PtoUlt3V0CI)







No comments:
Post a Comment