sudo apt install nodejs npm
mkdir -p ~/webappreact
cd ~/webappreact
npm init -y
#Change the following file in ~/webappreact/package.json as
cat > ~/webappreact/package.json <<EOF
{
"name": "webappreact",
"version": "1.0.0",
"description": "",
"scripts": {
"glogin": "clasp login",
"glogout": "clasp logout",
"gcreate": "clasp create --title 'React Test Project' --rootDir ./apps-script",
"gpush": "clasp push",
"gpull": "clasp pull",
"gstart": "clasp push --watch",
"build": "parcel build src/index.html --dist-dir ./apps-script",
"start": "parcel src/index.html --dist-dir ./apps-script"
},
"keywords": [],
"author": "",
"license": "ISC"
}
EOF
# install dependencies
npm install -D @google/clasp
npm install -D @types/google-apps-script # if you use VS Code Editor in ChromeOS
npm install -D parcel
npm install react react-dom
mkdir -p ~/webappreact/apps-script
# create ~/webappreact/apps-script/main.js as
cat > ~/webappreact/apps-script/main.js <<EOF
function doGet() {
return HtmlService.createTemplateFromFile("index")
.evaluate()
.addMetaTag("viewport","width=device-width, initial-scale=1.0")
}
EOF
mkdir -p ~/webappreact/src
# create ~/webappreact/src/index.html as
cat > ~/webappreact/src/index.html <<EOF
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Document</title>
</head>
<body>
<div id="app"></div>
<script type="module">
import "./index.js"
</script>
</body>
</html>
EOF
# create ~/webappreact/src/index.js as
cat > ~/webappreact/src/index.js <<EOF
import React from "react"
import App from "./App"
import { createRoot } from 'react-dom/client';
const container = document.getElementById('app');
const root = createRoot(container);
root.render(<App />, app)
EOF
# create ~/webappreact/src/App.js as
cat > ~/webappreact/src/App.js <<EOF
function App() {
return <div>
<h1>First React App</h1>
<p>Hello World</p>
</div>
}
export default App
EOF
# Testing building
cd ~/webappreact
npm run build
# Testing running in localhost:1234
# For Chrome Browser, please install React Developer Tools in chrome web store for testing at localhost
npm run start
# Login in to google apps script
npm run glogin
# Create Project in google apps script and choose spreadsheet
npm run gcreate
mv ~/webappreact/apps-script/.clasp.json ~/webappreact/
# Push to google apps script
npm run gpush
mkdir -p ~/webappreact/src/styles/
#Add ~/webappreact/src/styles/main.scss as
cat > ~/webappreact/src/styles/main.scss <<EOF
h1 {
color:green;
font-size: 2rem;
}
p {
color:purple;
}
.css-nav {
padding-left: 15px;
padding-right: 15px;
}
EOF
# change ~/webappreact/src/index.html as
cat > ~/webappreact/src/index.html <<EOF
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Document</title>
<style>
@import "./styles/main.scss";
</style>
</head>
<body>
<div id="app"></div>
<script type="module">
import "./index.js"
</script>
</body>
</html>
EOF
# install dependencies
npm install react-router-dom@6
mkdir -p ~/webappreact/src/components
# create ~/webappreact/src/components/Home.js as
cat > ~/webappreact/src/components/Home.js <<EOF
function Home() {
return <>
<h1>HomePage</h1>
</>
}
export default Home
EOF
# create ~/webappreact/src/components/About.js as
cat > ~/webappreact/src/components/About.js <<EOF
function About() {
return <>
<h1>About</h1>
</>
}
export default About
EOF
# create ~/webappreact/src/components/Nav.js as
cat > ~/webappreact/src/components/Nav.js <<EOF
import { Link } from "react-router-dom"
function Nav() {
return <>
<span className="css-nav"><Link to="/">Home</Link></span>
<span className="css-nav"><Link to="/about">About</Link></span>
</>
}
export default Nav
EOF
# change ~/webappreact/src/index.js as
cat > ~/webappreact/src/index.js <<EOF
import React from "react"
import { BrowserRouter } from "react-router-dom"
import App from "./App"
import { createRoot } from 'react-dom/client';
const container = document.getElementById('app');
const root = createRoot(container);
root.render(<BrowserRouter><App /></BrowserRouter>)
EOF
# change ~/webappreact/src/App.js as
cat > ~/webappreact/src/App.js <<EOF
import { Routes, Route } from "react-router-dom"
import Home from "./components/Home"
import About from "./components/About"
import Nav from "./components/Nav"
function App() {
return <>
<Nav />
<Routes>
<Route path="/" element={<Home />} />
<Route path="about" element={<About />} />
<Route path="*" element={<Home />} />
</Routes>
</>
}
export default App
EOF
# Testing building
cd ~/webappreact
npm run build
# Testing running in localhost:1234
npm run start
# Push to google apps script
npm run gpush
# test again in webapp of Google Apps Script
# Change ~/webappreact/apps-script/main.js as
cat > ~/webappreact/apps-script/main.js <<EOF
function doGet() {
return HtmlService.createTemplateFromFile("index")
.evaluate()
.addMetaTag("viewport","width=device-width, initial-scale=1.0")
}
function getData() {
return (
[{
"key": "apple",
"value": "green"
},
{
"key": "banana",
"value": "yellow"
}]
);
}
function getSpreadData() {
return SpreadsheetApp
.getActiveSpreadsheet()
.getActiveSheet()
.getDataRange()
.getValues();
}
EOF
# Change ~/webappreact/src/components/About.js as
cat > ~/webappreact/src/components/About.js <<EOF
import React, {useState, useEffect} from "react"
function About() {
const [data,setData] = useState(null)
const [loading, setLoading] = useState(false)
if (typeof google === 'object') {
useEffect(()=>{
setLoading(true)
google.script.run.withSuccessHandler(response => {
setData([...response])
setLoading(false)
}).withFailureHandler(er => {
alert(er)
}).getData()
},[])
}
else {
return <>
<h1>About</h1>
<table>
<tbody>
<tr>
<td><span style={{paddingLeft:'30px',paddingRight:'30px'}}>key: row.key</span></td>
<td><span style={{paddingRight:'30px'}}>value: row.value</span></td>
</tr>
</tbody>
</table>
</>
}
if (loading) return <h1>loading...</h1>
if (!data) return null;
return <>
<h1>About Data</h1>
<table>
<tbody>
{
data.map((row) => (
<tr>
<td><span style={{paddingLeft:'30px',paddingRight:'30px'}}>key: {row.key}</span></td>
<td><span style={{paddingRight:'30px'}}>value: {row.value}</span></td>
</tr>
))
}
</tbody>
</table>
</>
}
export default About
EOF
# Testing building and Push to google apps script
cd ~/webappreact
npm run build && npm run gpush
# test again in webapp of Google Apps Script
cd /boot/efi/EFI mkdir -p BOOT cp /boot/efi/EFI/kali/grubx64.efi /boot/efi/EFI/BOOT/BOOTx64.efi
# to install hashcat cd $HOME/Downloads git clone https://github.com/hashcat/hashcat.git cd hashcat git fetch --all --tags git checkout tags/v5.1.0 -b v5.1.0-branch make # don't make install # print version ./hashcat --version # print help ./hashcat --help # run benchmark ./hashcat -b -m 2500 -w 3 -d 1
# to install hashcat-utils cd $HOME/Downloads git clone https://github.com/hashcat/hashcat-utils.git cd hashcat-utils/src make # don't make install # print help ./cap2hccapx.bin --help # install hcxdumptool & hcxtools git clone https://github.com/ZerBea/hcxdumptool cd hcxdumptool/ make # don't make install git clone https://github.com/ZerBea/hcxtools cd hcxtools / make # don't make install https://gist.github.com/Nav-Appaiya/b8eb3cbf22642aac2ead12884fb6aa80
cd ~/Downloads tar -Jxvf amdgpu-pro-20.20-1098277-ubuntu-20.04.tar.xz cd amdgpu-pro-20.20-1098277-ubuntu-20.04 # change line 147based on above ./amdgpu-install -y --uninstall ./amdgpu-install -y --opencl=legacy --headless --no-dkms
network={
ssid="homenet"
psk=68002fbdacc8812f89c06a2fb6542b2b1126853983a59e0076e5f56df9c5543b
id_str="home"
priority=2
}
Get wpa_passphase from linux package wpasupplicant
network={
ssid="MyHomeWifi"
psk=6ac0d834a918dfdb09c7d4581a1665f5f1969ef3967e25cd932eab7c75075d54
id_str="home"
priority=2
}
iface home inet dhcpModify to fixed IP for home
iface home inet static
address 192.168.1.79
netmask 255.255.255.0
gateway 192.168.1.1
# reading passphrase from stdin
network={
ssid="mobile-1"
psk=2b975ade78236c65480641296127688b223b1270e7ce175e7317b5bf6ca4795a
id_str="mobile-1"
priority=4
}
Modify to, after running wpa_passphrase "Samsung S22" "mysecretwords"
network={
ssid="Samsung S22"
psk=6136bd9f2dced6eced7ec23dc4abed6d8dcff707a148d150ab97905facb6ca33
id_str="mobile-1"
priority=4
}
iface mobile-1 inet static
address 192.168.43.254
netmask 255.255.255.0
gateway 192.168.43.1
Modify to DHCP IP address for mobile-1iface mobile-1 inet dhcp
ssh kali@192.168.1.79
ssh kali@192.168.99.121
sudo apt update sudo dpkg-reconfigure tzdata sudo dpkg-reconfigure locales
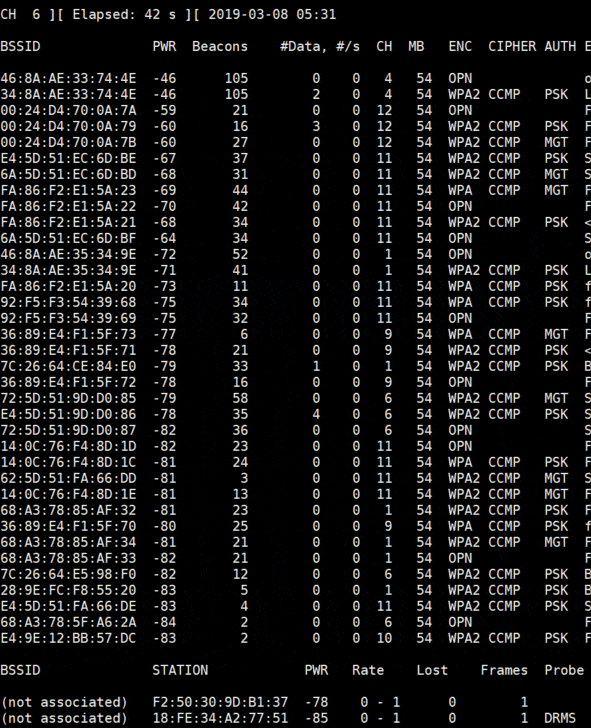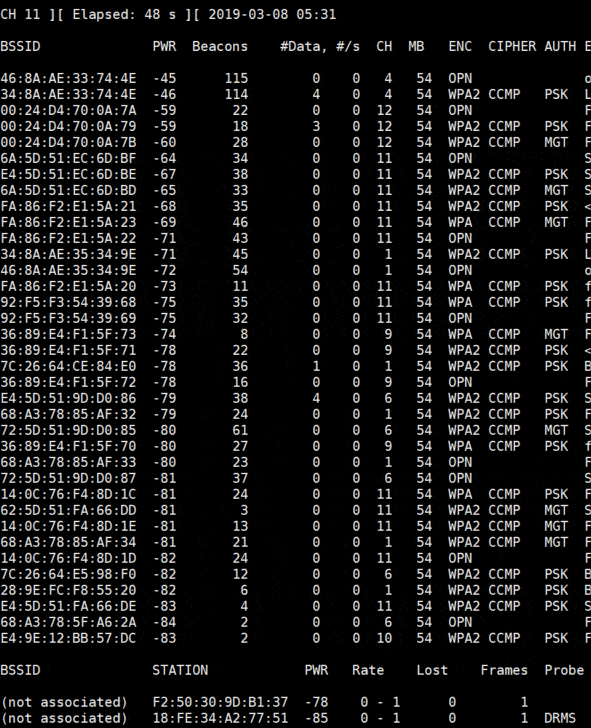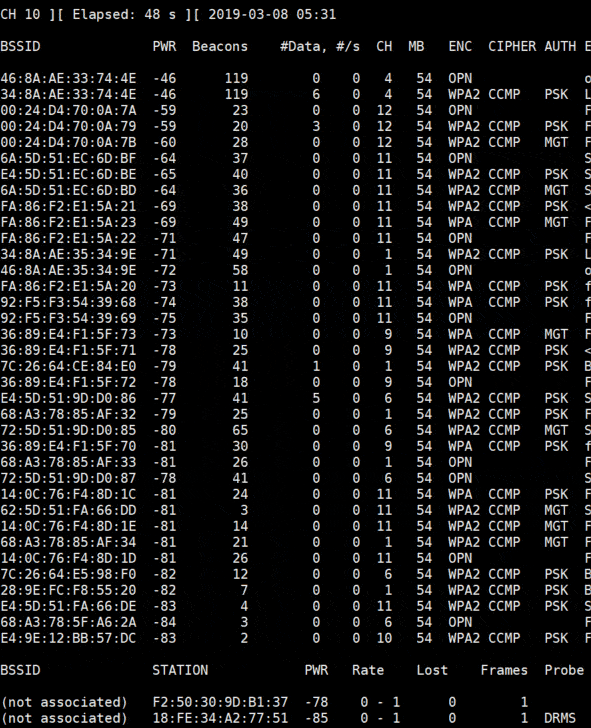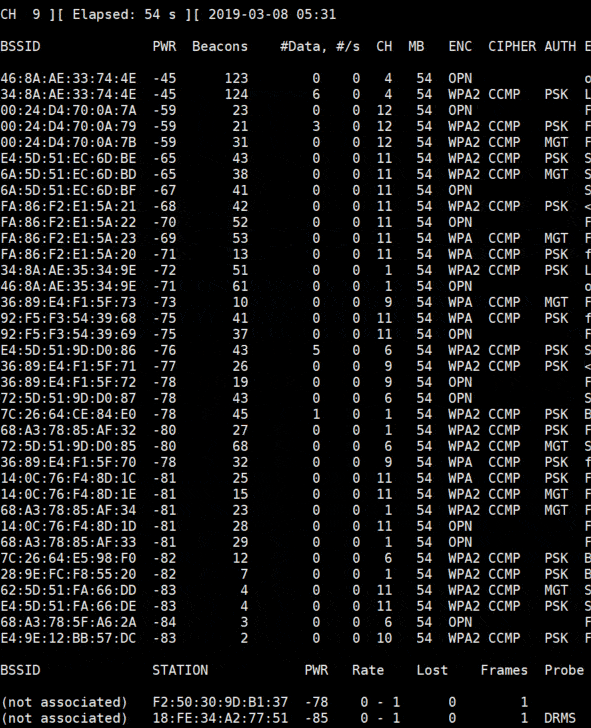
sudo mon0up sudo airmon-ng sudo airodump-ng mon0 sudo airodump-ng mon0 --bssid 34:8A:AE:33:74:4E --channel 4 --write mydump
if loadfont /boot/grub/font.pf2 ; then
set gfxmode=auto
insmod efi_gop
insmod efi_uga
insmod gfxterm
terminal_output gfxterm
fi
set menu_color_normal=white/black
set menu_color_highlight=black/light-gray
set timeout=5
menuentry "Ubuntu 20.04 persistence" {
set gfxpayload=keep
linux /casper/vmlinuz file=/cdrom/preseed/ubuntu.seed persistent fsck.mode=skip quiet splash ---
initrd /casper/initrd
}
menuentry "Ubuntu (safe graphics)" {
set gfxpayload=keep
linux /casper/vmlinuz file=/cdrom/preseed/ubuntu.seed maybe-ubiquity quiet splash nomodeset ---
initrd /casper/initrd
}
menuentry "OEM install (for manufacturers)" {
set gfxpayload=keep
linux /casper/vmlinuz file=/cdrom/preseed/ubuntu.seed only-ubiquity quiet splash oem-config/enable=true ---
initrd /casper/initrd
}
grub_platform
if [ "$grub_platform" = "efi" ]; then
menuentry 'Boot from next volume' {
exit 1
}
menuentry 'UEFI Firmware Settings' {
fwsetup
}
fi
{
"persistence": [
{
"image": "/iso/ubuntu-20.04.4-desktop-amd64.iso",
"backend": [
"/persistence/persistence_ext4_4GB_casper-rw.dat"
],
"autosel": 1,
"timeout": 10
}
] ,
"conf_replace": [
{
"iso": "/iso/ubuntu-20.04.4-desktop-amd64.iso",
"org": "/boot/grub/grub.cfg",
"new": "/ventoy/ubuntu.cfg"
}
]
}
